Estimate a phi function, and output omega
estRitaProperties.RdEstimate a phi function, and output omega
estRitaProperties(
phidat,
maxT,
bigT,
dt = 1/365.25,
min_dt = FALSE,
formula,
family,
use_geese,
return_all = FALSE,
plot_phi = FALSE,
...
)Arguments
- phidat
Data frame used to estimate the phi function, needs to have columns ri (recency indicator), ui (duration), and id (if use_geese == TRUE)
- maxT
Maximum time to estimate phi until
- bigT
T for estimating MDRI (what defines recent infection)
- dt
An integration step size. Should be no more than 1 day.
- min_dt
Make the minimum time dt (necessary if doing a log transformation of ui)
- formula
Formula for fitting the model to phidat. Formula argument must take in only ui as the newdata. For example, do not create a ui^2 variable. Use poly(ui, ...) function to fit polynomial terms.
- family
Family argument for glm or gee
- use_geese
Indicator to fit a gee model using geese(), or a glm model with glm()
- return_all
Whether to return additional objects used in internal functions (will use more memory)
- plot_phi
Whether or not to plot the estimated phi function
- ...
Additional arguments to glm or geese for fitting model
Value
List of results:
omega: Estimate of Omegaomega_var: Variance of estimate of OmegabigTidx: Index of bigT based onts_indexts_index: Index mapping each time point to an integerget.integral.est: Function to give an estimate of Omega T for some T as arg to the function
Examples
# Define phi function
phi.func <- getTestRecentFunc(window=200, shadow=191)
# Simulate external study data
study <- simExternal(1, phi.func)
colnames(study) <- c("id", "ui", "ri")
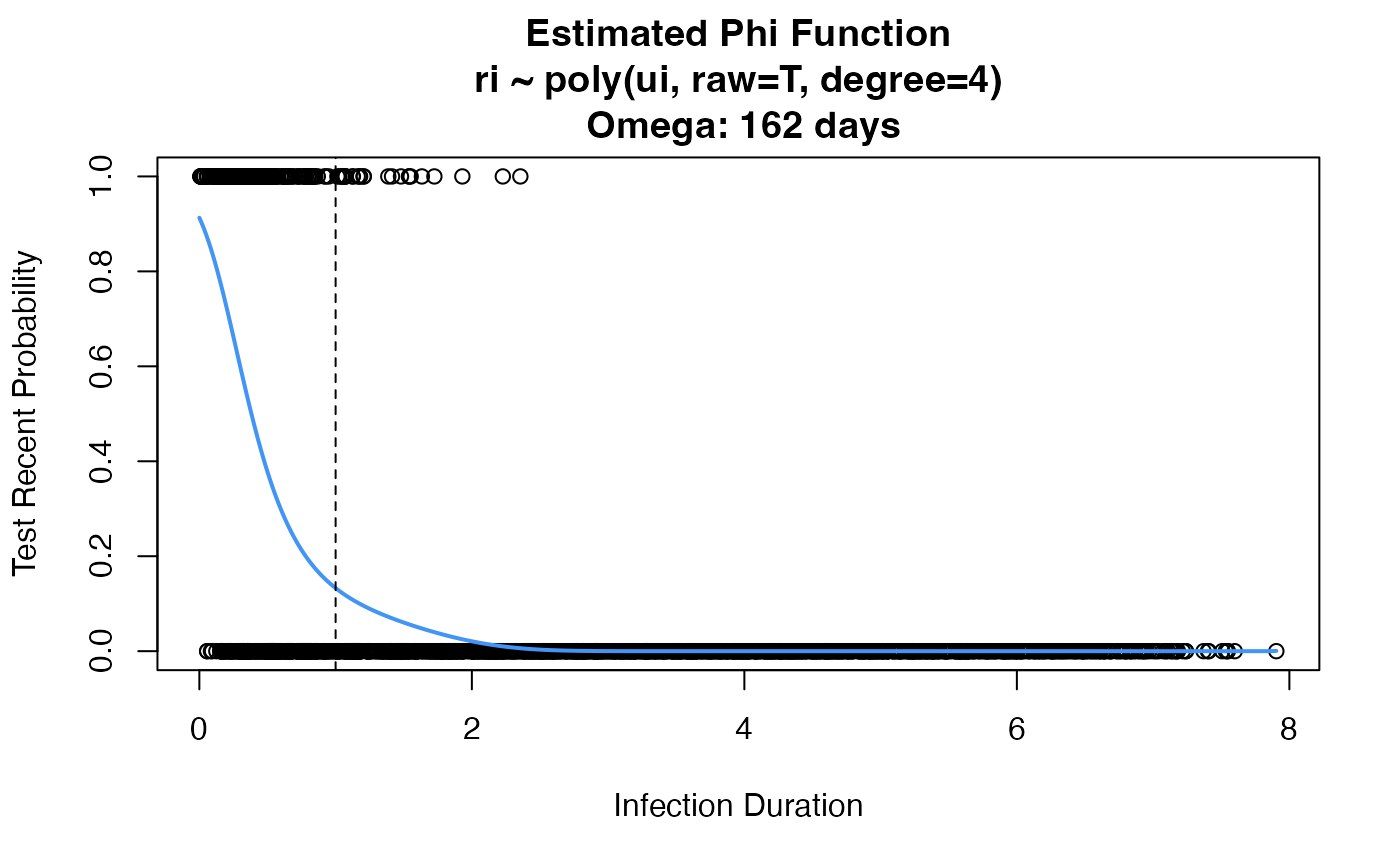
# Estimate omega based on 3rd degree polynomial
props <- estRitaProperties(
phidat=study, maxT=5, bigT=1,
formula="ri ~ poly(ui, raw=T, degree=4)", family=binomial(link="logit"),
use_geese=TRUE, plot_phi=TRUE, return_all=TRUE)
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
 # Estimate omega based on 3rd degree polynomial, log function
# NOTE: If you do this, need to not have any ui = 0
study.log <- study
study.log[study.log$ui == 0, "ui"] <- 0.01
props <- estRitaProperties(
phidat=study.log, maxT=10, bigT=1, min_dt=TRUE,
formula="ri ~ poly(log(ui), raw=T, degree=4)", family=binomial(link="logit"),
use_geese=TRUE, plot_phi=TRUE)
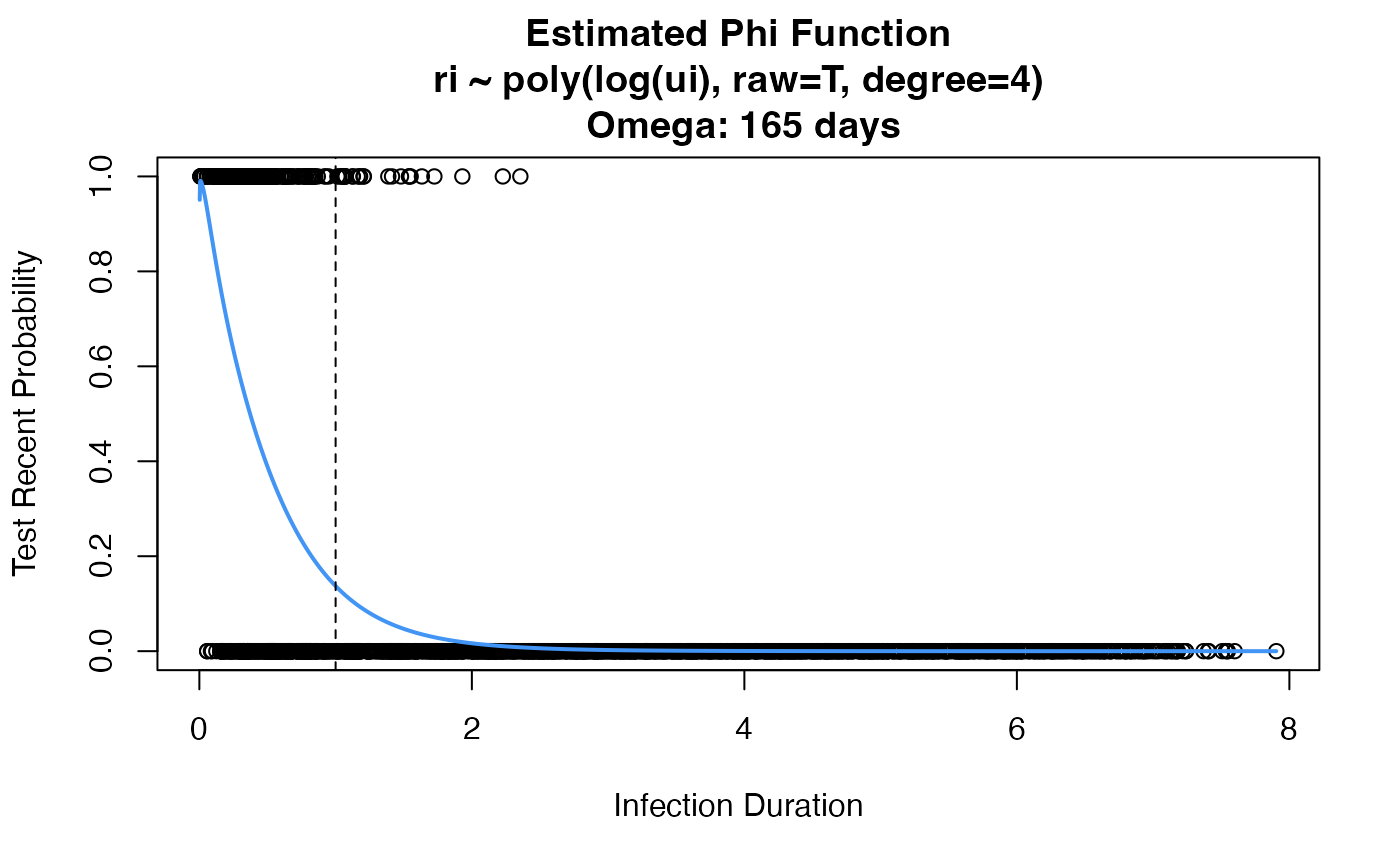
# Estimate omega based on 3rd degree polynomial, log function
# NOTE: If you do this, need to not have any ui = 0
study.log <- study
study.log[study.log$ui == 0, "ui"] <- 0.01
props <- estRitaProperties(
phidat=study.log, maxT=10, bigT=1, min_dt=TRUE,
formula="ri ~ poly(log(ui), raw=T, degree=4)", family=binomial(link="logit"),
use_geese=TRUE, plot_phi=TRUE)
 # Return additional function that can be used to
# quickly get other omega estimates
props <- estRitaProperties(
phidat=study, maxT=5, bigT=1,
formula="ri ~ poly(ui, raw=T, degree=3)", family=binomial(link="logit"),
use_geese=TRUE, plot_phi=FALSE, return_all=TRUE)
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
# What is \int_0^T \phi(t) dt for ts=T?
props$get.integral.est(ts=2.1)
#> $omega
#> [1] 0.5092978
#>
#> $omega_var
#> [1] 0.0004007974
#>
#> $idx
#> [1] 767
#>
# Return additional function that can be used to
# quickly get other omega estimates
props <- estRitaProperties(
phidat=study, maxT=5, bigT=1,
formula="ri ~ poly(ui, raw=T, degree=3)", family=binomial(link="logit"),
use_geese=TRUE, plot_phi=FALSE, return_all=TRUE)
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
# What is \int_0^T \phi(t) dt for ts=T?
props$get.integral.est(ts=2.1)
#> $omega
#> [1] 0.5092978
#>
#> $omega_var
#> [1] 0.0004007974
#>
#> $idx
#> [1] 767
#>