Snapshot and Adjusted Estimators • XSRecency

library(XSRecency)

In this vignette, we show how to use the snapshot and adjusted estimators for cross-sectional incidence estimation. First, we will simulate cross-sectional data using functions from within this package. Then we illustrate how to use the estimation functions.

Simulate Cross-Sectional Data

Define a test-recent function

# Create an test recent function that approximates the following window and shadow period
# getTestRecentFunc() takes in window and shadow period in days as arguments
phi.func <- getTestRecentFunc(window=200, shadow=191)

ts <- seq(0, 10, by=0.01)
plot(phi.func(ts) ~ ts, type='l')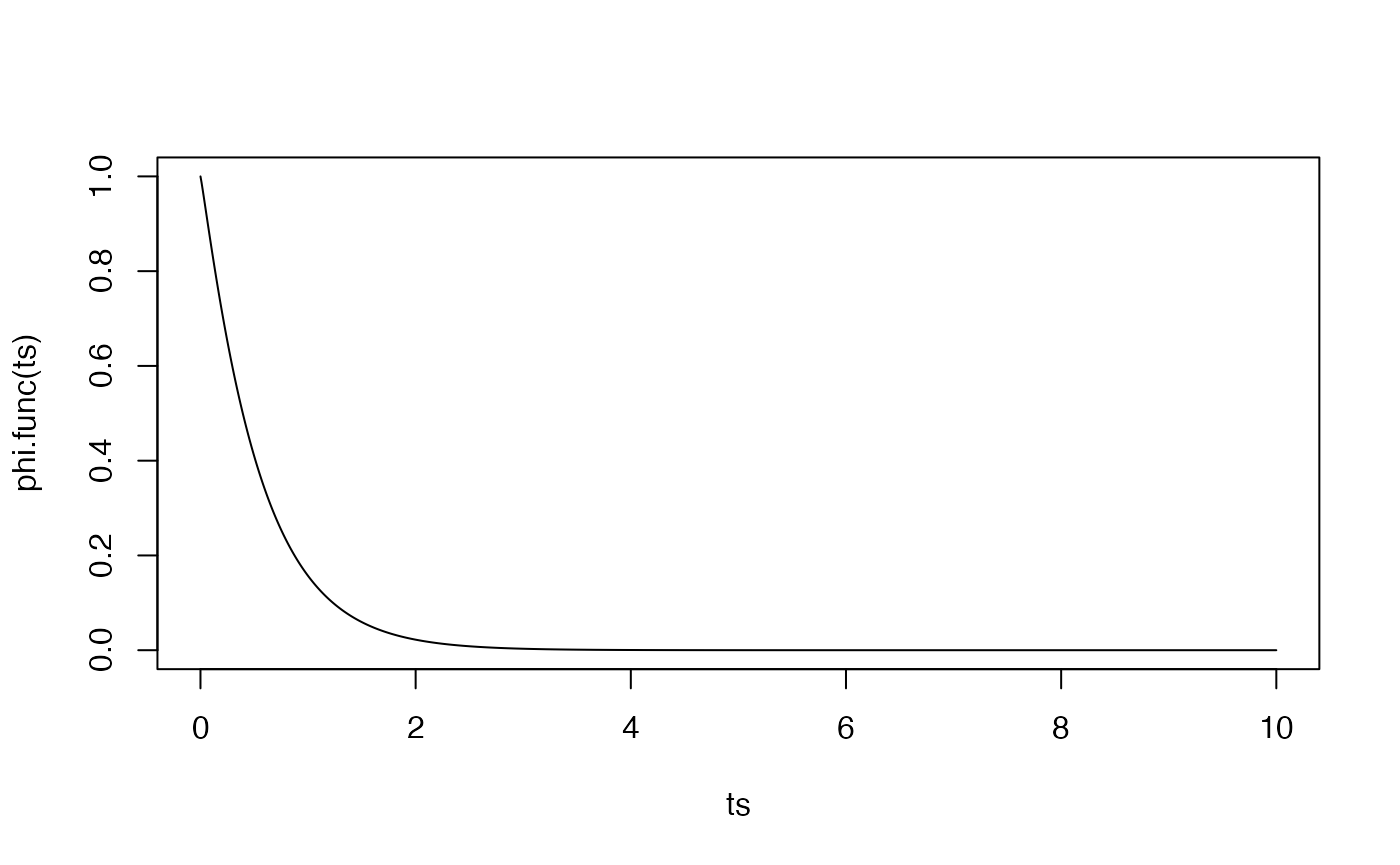


# Calculate the MDRI at 2 years for this function (we know that the window is 200/365.25)
window <- 200/365.25
mdri <- integratePhi(phi.func, maxT=2)
mdri
#> [1] 0.5363007

Simulate cross-sectional data based on constant incidence of 0.032 and prevalence of 29%.

sim <- simCrossSect(phi.func=phi.func,
                    incidence_type="constant", prevalence=0.29, baseline_incidence=0.032)

set.seed(10)
data <- sim(5000)
head(data)
#>   di ui ri
#> 1  0 NA NA
#> 2  0 NA NA
#> 3  0 NA NA
#> 4  0 NA NA
#> 5  0 NA NA
#> 6  0 NA NA
tail(data)
#>      di         ui ri
#> 4995  1  5.4014360  0
#> 4996  1 10.3831010  0
#> 4997  1 12.6781044  0
#> 4998  1  0.5060816  1
#> 4999  1  1.0612372  0
#> 5000  1  7.8467520  0

Records with are HIV-negative individuals, and are positive individuals. The variables and are infection times (based on epidemiological parameters supplied) and recent infection indicators (based on the phi function), respectively.

Apply Estimator

Snapshot Estimator

estSnapshot(n_r=sum(data$ri, na.rm=T), n_n=sum(!data$di), n_p=sum(data$di), n=5000,
            mu=window, mu_var=0)
#> $est
#> [1] 0.03369465
#> 
#> $var
#> [1] 1.778887e-05

In some scenarios, not all individuals who test positive for HIV will receive a test. Here we show how to apply the estimator in these cases, using the argument n_p_test. The same argument can be used in the estAdjusted function.

# Remove 50% of the recency tests to simulate what would happen if only 50% of
# HIV positive individuals received a recency test
data$mask <- rbinom(n=5000, size=1, prob=0.5)
data$ri_mask <- data$ri
data[data$mask == 1, "ri_mask"] <- NA

estSnapshot(n_r=sum(data$ri_mask, na.rm=T), n_n=sum(!data$di), n_p=sum(data$di), n=5000,
            mu=window, mu_var=0, n_p_test=sum(data$di & (!is.na(data$ri_mask))))
#> $est
#> [1] 0.03823064
#> 
#> $var
#> [1] 3.89342e-05

Adjusted Estimator

# Suppose the FRR was known to be 0.1%
estAdjusted(n_r=sum(data$ri, na.rm=T), n_n=sum(!data$di), n_p=sum(data$di), n=100,
            omega=mdri, omega_var=0, beta=0.001, beta_var=0, big_T=2)
#> $est
#> [1] 0.0337468
#> 
#> $var
#> [1] 1.755951e-05

References

Kaplan, E. H., & Brookmeyer, R. (1999). Snapshot Estimators of Recent HIV Incidence Rates. Operations Research. 47(1): 29–37. doi:10.1287/opre.47.1.29
Kassanjee, R., McWalter, T. A., Bärnighausen, T., & Welte, A. (2012). A New General Biomarker-based Incidence Estimator. Epidemiology. 23(5): 721–728. doi:10.1097/EDE.0b013e3182576c07